You'll catch your death!

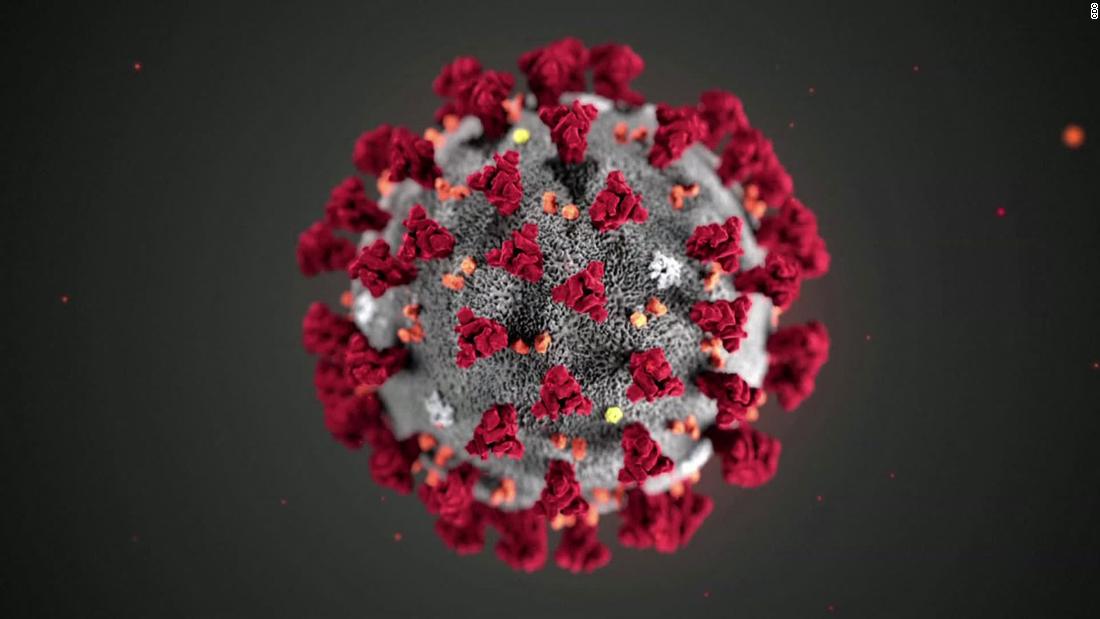
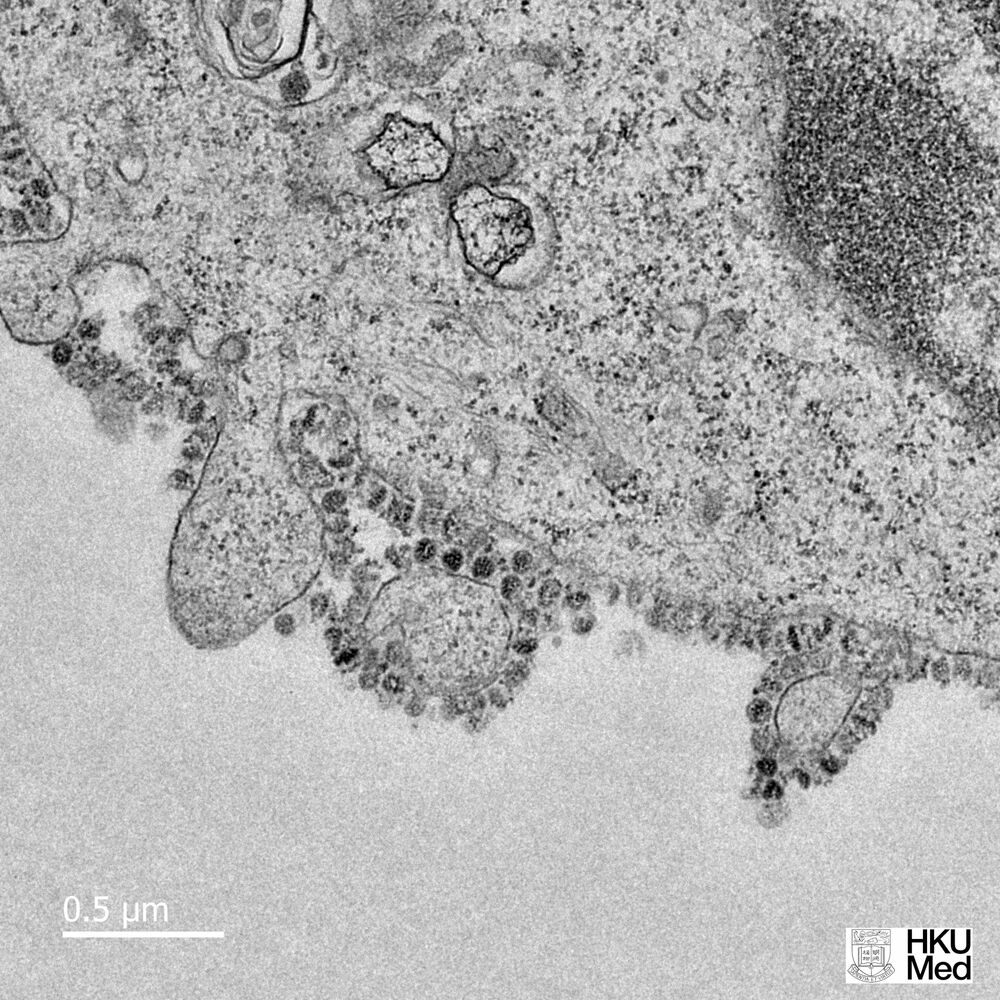
Years ago, when I was a schoolboy, in particular when it was a cold, wet winter's day, my mother would stop me on my way out of the door, look at how unsuitably dressed I was, and make it clear that if I went out dressed like that I would be sure to catch my death! This is a saying that dates back to the seventeeth century: my mother was born in the 1920s and her lessons in life and childcare skills were largely handed down from her mother from generation to generation, as was and still is the case for many families. As I got older, I managed to fob her off; but was she right? 

Read the following. Then ask yourself, where have you heard the same thing recently?

...is a viral infectious disease of the upper respiratory tract that primarily affects the nose. The throat, sinuses and larynx may also be affected. Signs and symptoms may appear less than two days after exposure to the virus. These may include coughing, sore throat, runny nose, sneezing, headache and fever. People usually recover in seven to ten days, but some symptoms may last up to three weeks. Occasionally those with other health problems may develop pneumonia...spread through the air during close contact with infected people or indirectly through contact with objects in the environment, followed by transfer to the mouth or nose. ...The symptoms are mostly due to the body's immune response to the infection rather than to tissue destruction by by the viruses themselves.

There is no vaccine... The primary methods of prevention are hand-washing; not touching the eyes, nose or mouth with unwashed hands; and staying away from sick people. Some evidence supports the use of face masks. There is no cure....^[

It comes from the Wikipedia article on the common cold, but with a few minor changes it could be describing Covid-19. The take-home message is clear, viruses (in the case of most colds they are caused by rhinoviruses (think rhinoceros: Greek for nose and horn) have been around a long time and they aren't likely to give up any time soon. Moreover while our immune system can deal with some viruses, it is clear that in some cases we will catch our death! In order to meet the challenge of these molecular parasites we need to understand a little about their way in which they spread through populations.

By now, you will be aware of the general molecular and cellular features of a virus, so let's take a look at the mathematics underpinning the predictions that we have been hearing so much about in the media. The curve on the right was the subject of many of the early government messages centred around the phrase: "we need to flatten the peak". If I separate the curve into three phases (the early, middle and late phases, from left to right), the first third is the exponential phase, in which the number of cases (in this example) increase dramatically after an initial "lag phase". Those of you studying Biology will be familiar with this relationship, since it is commonly used to illustrate the doubling time or growth rate of bacteria.

James (my PhD student) kindly produced a simulation of bacterial growth for me this morning (shown left) in which the doubling time is set at a range of theoretical times from 5 to 30 minutes (for illustrative purposes). The important point to note is that the lag phase and the steepness of this curve is a function of (is directly related to) the replication rate of the organism (another way of expressing the doubling time). The graph could be used to show how temperature influences growth rate, availability of nutrients or types of nutrients, pH etc. It could also show how individual species in a mixed culture grow at different rates. In other words the approach to the "exponential phase" and the steepness of this phase are  two of issues that the Government's Chief Scientist and Medical Officer were Government in trying to delay the peak of infection.

In the context of the spread of Covid-19 infections, the axes on the Government plot are numbers of infected individuals (y) versus days after the initial report of the outbreak (x). As I am sure you can appreciate, one infected person will infect a number of others, in a manner that is dependent on the frequency of personal encounters, the length of time of those encounters and the immunity of the individuals in that group. For every type of virus, there is a so called viability factor often expressed in days, which relates to the time dependent decay in the infectivity of an isolated virus particle as it sits on a particular surface. It seems that viruses last about twice as long on a solid surface compared with clothes, and the general consensus published in the New England Journal of Medicine is that infectivity lasts for a maximum of 72 hours. 

When these and some other less critical factors are combined, predictions can be made about the rate of spread of the virus and its likely progression throughout a community. In the early stages, where no immunity exists (no vaccine and a new virus), the lag phase will be short and the exponential phase will be steep. In order to flatten the curve, the Government (in the case of the UK) have introduced a series of increasingly stringent public order measures. As you will see from the two curves (flat and sharp) the area under the curves is approximately the same. The Government's public isolation measures are not likely to reduce the total number of individuals infected significantly, but rather to slow the pace of the spread. The reduction in cases will follow as a level of herd immunity develops. The main purpose of the Government measures  is to make it possible for the healthcare sector to manage the outbreak in the most effective way, and hopefully this will reduce the number of deaths. I was first made aware of the need to flatten peaks when I saw the graphs of electricity usage during televised events like a major cup final. Everyone puts on the kettle at half-time! Interestingly, the shift from real time TV to streaming and downloads to other devices has significantly altered public behaviour, and the peak of power usage associated with the prime time TV slot for many years has flattened considerably. Clearly public behaviour is a major factor in limiting the impact of a pandemic episode. 

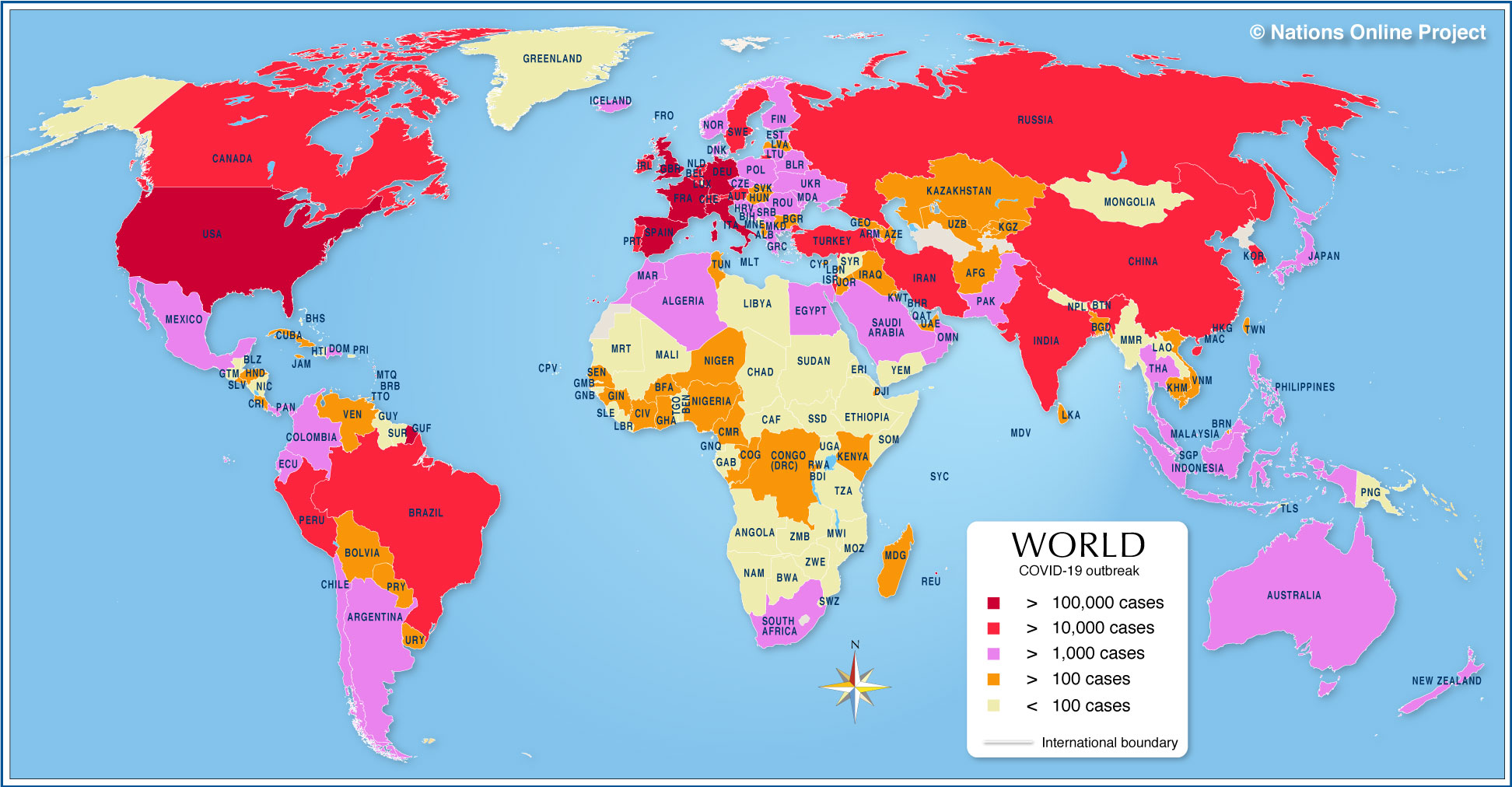The third phase of the curve is the decline of infected numbers: the moment we are all waiting for and the phase that nobody is willing to predict. The map on the right shows that China, the USA and Europe (in red) are approaching a peak, with African countries lagging behind. This is similar to the difference between bacteria that are slow and fast replicators (see the first graph above). In time the whole world map will be red, the absolute numbers will be a measure of the success of each country's management strategy. If nothing else, this will be the point at which we regroup and put measures in place order to limit the impact of a future pandemic. All of these discussion assume that there will not be a vaccine available to head the virus off at the pass. The reality is (as I discussed in my last post), that novel viruses will always present a major threat to global health and the development of effective vaccines is not something that can be guaranteed, and why I believe this is an area that warrants a major investment. 

So returning to the title of the post, how likely is it that your will catch your death from the common cold viruses. The answer is highly unlikely. However, the same is not true for Covid-19, as we are finding out.The most common cause of colds, rhinoviruses were only first recognized as the cause in 1956, by Winston Harvey Price. The virus is not enveloped (see left), like norovirus, and it recognises a cell surface protein called ICAM 1, which you can read about here. The questions that immediately spring to my mind next are

• Can we expect to conquer viruses with antivirals? 

• How do viruses evoke different responses in humans?

I shall tackle the first question in my next post and then prepare myself for the challenge of explaining immunological response pathways and our current understanding of why some people have mild symptoms when infected with Covid-19 and for some it is lethal!

Update

I noticed that on the BBC News website yesterday, there was an explanation of the graphical data (published daily by Johns Hopkins University Epidemiology Unit). They posted two graphs (see below)

Graph 1

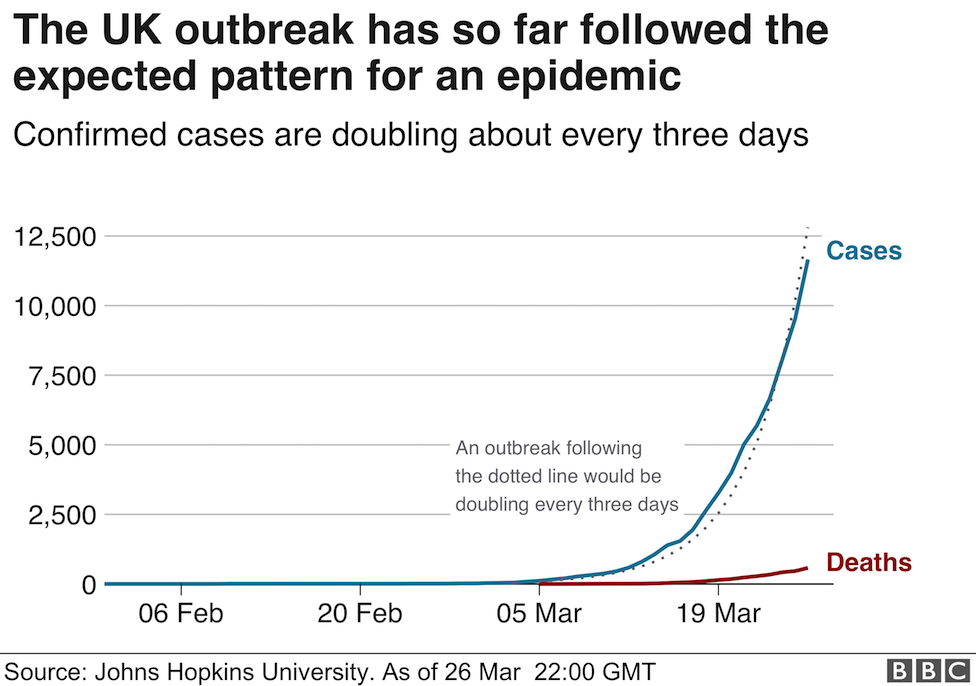
Graph 2

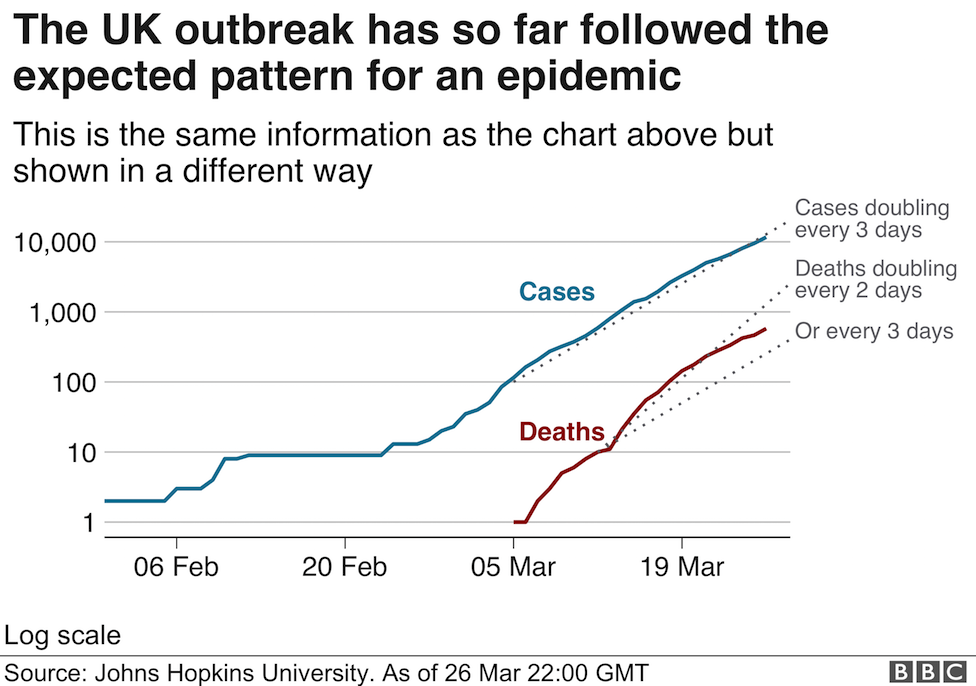
Can you see what they have done to illustrate the time dependent growth of cases? The second graph is a semi-log plot (look here if you need more!)in which the x axis remains linear and the y axis increases logarithmically. As a result the data tend towards a linear relationship (not quite, but with more data it would look smoother). As a student I would use log graph paper and semi log graph paper (with the term cycles used to indicate the number of log divisions) frequently: it made estimating gradients easy: today, the computer has eliminated the need! 

Covid-19 and the road to a vaccine

In my last post, I explained the basic properties of Covid-19 and how it relates to other well known viruses. Of perhaps the greatest concern to everyone is how science and medicine can be harnessed to beat this virus. There are currently a limited number of pharmacological ways of combating the pathological effect of a virus. The first one I am going to discuss is vaccination and in a separate post I shall focus on antiviral drugs. Antidotes represent a specialist category of medicines that are administered to reverse the effects of a toxin and I won't discuss them here (maybe later). One small point, after a few suggestions from readers, I have tried to explain key terms as I go along. If there is no explanation (eg endosomes) I am assuming these are not essential for general understanding and can easily be found via Google, for the aficionados!

The word vaccine is itself a little unusual, if you don't already know, it is derived from the Latin word vaccinus, pertaining to cows, which makes sense, since Jenner's work was based around cowpox. The World Health Authority's statement on vaccines captures the essence of their use in medicine:

"Vaccination is one of the most effective ways to prevent diseases. A vaccine helps the body’s immune system to recognize and fight pathogens like viruses or bacteria, which then keeps us safe from the diseases they cause. Vaccines protect against more than 25 debilitating or life-threatening diseases, including measles, polio, tetanus, diphtheria, meningitis, influenza, tetanus, typhoid and cervical cancer".

The small glass vials in the above image (typically sealed with a rubber stopper) are in universal use for storing vaccines before injection. But what is inside a typical vaccine? To the pharmacist, the way in which any medicine is packaged and prepared for administration is referred to as formulation. And in the case of vaccines, you may be surprised at the formulation. In addition to the recombinant mixture of antigens (it is directed at 4 molecular variants, or quadravalent), a vial of Afluria vaccine from Seqirus for example, also contains:

sodium chloride, monobasic sodium phosphate, dibasic sodium phosphate, monobasic potassium phosphate, potassium chloride, calcium chloride, sodium taurodeoxycholate, ovalbumin, sucrose, neomycin sulfate, polymyxin B, betapropiolactone, hydrocortisone thimerosal

...all of which are collectively referred to as adjuvants, or substances that enhance the immunogenicity of the vaccine's principle component. (To be precise, some components are adjuvants and others are stabilizers, that ensure the vaccine maintains its potency under the recommended storage conditions).

Three dimensional structure of haemagglutinin

Of course the key component of the vaccine is the immunogen, which is defined as an antigen that elicits an immune response. The word antigen itself is defined as a foreign molecule that specifically interacts with an antibody (you can read about antibodies at an earlier post). Antigens can be small molecules (where they are sometimes called haptens), proteins or whole cells. In the case of Afluria, the immunogens are given below by the manufacturer: each 0.5ml dose contains 15µg haemagglutinin (HA), total 60µg, from four influenza types and subtypes: A/H1N1, A/H3N2, B/Yamagata, and B/Victoria. The multi-dose vial also contains thimerosal (24.5µg mercury per 0.5ml dose). The image above on the LHS is a representation of haemagglutinin, one of the main immunogens used in influenza vaccines.

H(a)emagglutinin (UK/US spellings), as shown above projects outwards from the surface  of the virus particle. The four variants of HA (above in red) are mutants found associated with different viral strains. The quadravalent vaccine aims to eliminate all four major types of influenza in circulation. Why target haemagglutinin? To answer this  we need to understand how influenza virus acts on us. The influenza virus is shown schematically on the RHS. Covid-19 has a single major spike protein, but the flu virus has two: neuraminidase (N) and haemagglutinin. (This why you may hear of flu viruses called H1N1, which is a shorthand for a specific combination of haemagglutinin and neuraminidase sequences). 

Influenza virus HA first binds to sialic acid residues on glycoproteins or glycolilipid receptors on the surface of the host cell, in response, the cell then engulfs (or endocytoses) the virus. In the acidic environment of the endosomes, the virus changes shape and fuses its envelope with the endosomal membrane. This is followed by a signal to release the virus nucleocapsid into the host cytoplasm. From there, the nucleocapsid travels to the host nucleus and a train of events has now been triggered that leads to virus replication. Here is a nice video simulation of the process. Unlike the virus itself, a vaccine will stimulate the production of antibodies that will in turn block this sequence of events by masking the HA or N proteins.

Unfortunately, these proteins are susceptible to mutation (as discussed in the previous post) and, as a result, completely new vaccines must be prepared each year. The design of each new vaccine is determined following a twice yearly international consultation and evaluation of the epidemiology of viral infection and the determination of the genome sequences of the most common viruses. The time taken for a flu vaccine to be produced just fits into the "window" between the February (northern hemisphere) decision meeting and the surge in cases typical of flu in October as can be seen from the 1918 Spanish Flu pandemic (top LHS): we are unsure yet whether Covid-19 is seasonal. 

So here's what happens when you are injected with a flu vaccine (or any other vaccine for that matter). The formulated preparation of antigens stimulates the production (in this case ) of HA/N specific antibodies. Shortly after the injection some people experience mild flu-like symptoms, but importantly, within around 14 days, you will have produced a reservoir of antibodies that can be mobilized rapidly if you become infected with the virus in the future. You are now immune to the virus. [I shall come back to the issue of the level and the longevity of immunity later in the post.] I have given the example of influenza vaccination which is usually injected intra-muscularly, but a vaccine can be administered orally, subcutaneously (the needle penetrates the fatty tissue beneath the skin), intra-nasally (though the nose) or intra-venously. Again, each method will be associated with a specific formulation. 

Last week in the journal Science, a US structural biology group used cryo-electron microscopy to determine the structure of the Covid-19 spike protein, This is/will be the major vaccination target. The spike protein makes an interaction with a protein called ACE-2 (angiotensin converting enzyme-2: this enzyme is displayed on the membrane of cells from a number of tissue types including the lung, where it plays a role in lowering blood pressure). I hope you can see from one of the images taken from the paper that the spike protein (on the right) changes shape on making contact with the target cell. The green coloured domain adopts the "up position" revealing a surface that makes a strong interaction with ACE-2. At this point, the virus is engulfed and the viral RNA makes its way into the cytoplasm where a combination of transcription (producing the mRNA needed to manufacture new viral components) and replication takes place, as the virus overwhelms the cell. The race is on to produce a vaccine against the Covid-19 virus.

The time taken to produce a new vaccine is at least 18 months (allowing for design, manufacturing, safety testing and trials) to many years. The best flu vaccines available in 2020 offer at best around 50% protection against hospitalisation as a result of flu infection. Similarly, 40 years on from the emergence of HIV and AIDS, there is currently no vaccine that will prevent HIV infection, or treat those who have it. You may have heard about the Moderna  vaccine that is currently undergoing safety testing in volunteers (Phase I Cliical Trial). The innovation here is to bypass the need to purify the protein-based immunogen (or whole virus), by direct injection of the mRNA encoding the immunogen (the spike protein). The use of mRNA as the immunogen, which in some ways mimics the way in which Covid-19 operates, was first suggested nearly 30 years ago, but only in the last 10 years has technology been available to translate this concept into clinical practice. I will be watching the outcome of this work with great interest, but the likely availability of an effective vaccine is still at least a year away: and possibly longer.

As promised earlier, I said I would mention the durability of vaccines and vaccination. In the case of seasonal flu, those who are perceived to be most vulnerable are a priority for vaccination. [You will also have no doubt heard reports of deaths resulting from Covid-19 and their "underlying conditions". 
This is a catch-all phrase to emphasise that those most likely to experience life-threatening  consequences of infection,are those with an already challenged immune system. In addition, since Covid-19  gains entry via the respiratory system, among those at high risk will be chronic asthmatics and cystic fibrosis sufferers]. The durability of an individual's immune response seems to be variable. In addition each type of vaccine appears to show differences. There is a nice article here on the factors known to influence the longevity of a vaccine. Suffice to say though at this stage, in the absence of a Covid-19 vaccine, only time will tell.

I shall leave you with a link to a recent editorial in the journal Science, which  in my view makes some powerful and important observations on the need to ensure that we understand the underpinning Science and respect the fundamental laws of Nature that will eventually enable us to develop a vaccine. As Richard Feynman famously once said: 

"For a successful technology, reality must take precedence over public relations, for Nature cannot be fooled." 

Understanding Covid-19 . I Definitions and Origins

This is a short series of science oriented posts on the current Coronavirus pandemic. I intend to release them in bite-sized narratives and so there will be 3-4 to follow. All questions and comments welcome, but I should make it clear I am not a virology expert.


The subject on everyone's lips (hopefully metaphorically and not physically!) is the Corona virus pandemic. With a tsunami of information everywhere, I thought I would provide some background to the issues that have cropped up in my conversations with colleagues, students and friends. My emphasis will be scientific and not behavioural, but hopefully it will clarify some misconceptions and provide the facts as they relate to other historic viral epidemics. At the end of each post I shall provide a glossary to ensure you have a good working definition of key words (which I shall highlight in bold at the first mention). Ideally, these posts will serve as a resource and please feel free to post questions, which I will do my best to answer in a timely way. I shall begin with some generic properties of all known viruses and then I shall focus on some of the well known examples.

Let's begin with a the word virus itself, originating from Latin, where it was used to describe a poison from an animal such as a snake's venom. It was then in 1900 that medical researchers recognized that some infectious agents or particles could be selectively removed by simple filtering procedures. This provides the dictionary definition below with the reference to virus dimensions (20-300nm). Interestingly Google's Ngram analysis identifies the 1980-1995 period as the period of most frequent printed use of the word virus (I am betting this will be overtaken by 2015-2025, when it gets analysed!). My favourite definition is given below and was obtained from www.dictionary.com

A virus is an ultramicroscopic (20 to 300 nm in diameter), metabolically inert, infectious agent that replicates only within the cells of living hosts, mainly bacteria, plants, and animals: composed of an RNA or DNA core, a protein coat, and, in more complex types, a surrounding envelope.

Let's unpack some of these terms. Ultra-microscopic implies that the virus cannot be "seen" using a conventional "light microscope", used routinely to look at bacteria or human blood cells (for example). An electron microscope is required for direct visualization, and the image on the right was taken by researchers at the University of Hong Kong. The scale bar shows the virus (looking like a crown or corona from the Latin again, or ancient Greek for a wreath (classical scholars among you will be familiar with the Olympic victor's wreath, made from olive branches) entering a human cell prior to its reproduction. The white scale bar shows the diameter of the virus as approximately 500nm (slightly larger than the dictionary definition). The virus genome will be discussed later, but the term metabolically inert refers to the fact that viruses of this kind are absolutely dependent on the host for providing energy (in the form of ATP) for their reproduction (often called replication): they cannot produce energy from food: they "steal" it from the host. The terms RNA, DNA, protein (coat and envelope) describe the classes of macromolecules associated with information (RNA and not DNA in the case of covid-19), structural and catalytic components (proteins) and the "protective shell" or envelope surrounding the virus particle.

In short then, covid-19 is an RNA virus capable of infecting humans primarily through a respiratory route (nose and mouth). It is around 500nm in diameter (a typical lung cell has a diameter of 8000nm: assuming viruses and cells are perfect spheres, what would be their respective volumes and what would be the capacity of each cell for virus particles?). It is an enveloped virus surrounded by a lipid membrane, into which a number of major "spike" proteins are embedded. It is these spike proteins that establish contact with respiratory cells prior to invasion of the cell itself (as shown above). The spike protein will assume importance in subsequent discussions of vaccination strategies.

The leaf on the left is healthy, but the one on the
right has been overwhelmed by a TMV infection

The first detailed analysis of any RNA virus was the subject of the 1946 Nobel Prize awarded to three protein scientists, including Wendell Stanley for his work on Tobacco Mosaic Virus (TMV). In a seminal paper published in 1935 (yes 85 years ago!). Stanley purified and crystallized this cylindrical virus and demonstrated that the pure preparation could elicit the biologically common infection of tobacco plant leaves as shown in the image on the left. In 1935, proof that DNA was the genetic material was unavailable, and moreover, methods did not exist to easily identify and characterize RNA molecules. Today we know that some of the major pathogenic viruses are encoded by RNA and not DNA genomes.

The diagram on the right, compares the structural features of covid-19 (left) and TMV (middle)  alongside another well known pathogen, the norovirus. These three viruses share some things in common, but covid-19 (like HIV) is an enveloped virus: the other two have capsids not envelopes and importantly, alcohol gel is ineffective in eradicating norovirus, but effective at inactivating covid-19. In general hand-washing with soap is the best way to reduce viral transmission, since the viruses we are likely to encounter could be of either type. All RNA viruses that infect eukaryotic host cells (plant or animal) must either express their genes from the injected RNA by direct transcription, or by first converting the RNA genome into DNA, through the action of the enzyme Reverse Transcriptase. With the viral genome now in the form of DNA, the host cell machinery that converts its own structural genes into first mRNA and then proteins, is hijacked by the virus genome. The result is a rapid accumulation of the building blocks needed to make more virus particles. When the cell capacity is exceeded, the infectious particles are released and the host begins to mount an immune defence. (I shall discuss this process in the light of the recent work published by the Australian virology group, but I do like this NYT graphic summary).

To end this first installment, one question I have been asked is "how does covid-19 compare with small-pox virus"? By the end of the eighteenth century, smallpox was responsible for killing around 10% of the world population..... and then along came Edward Jenner (here is one link that looks at the historical eradication of smallpox). The origins of variola virus (the cause of small pox and cow pox) are unknown, but certainly date back to the third century BCE. Variola viruses are unlike covid-19 in one important respect: they are DNA viruses. Why is this important? Viruses encoded by DNA genomes are less likely to mutate than RNA viruses, since the process of viral genome replication is less "error-prone" in DNA viruses and therefore the equivalents of the "spike proteins" in variola viruses present an easier target for vaccine production. For this reason, unlike flu vaccines, which are produced seasonally, smallpox vaccines can be stockpiled through the agency of the World Health Organisation (a valuable resource in all ways). There are over 30m shots of vaccine in deep storage, just in case this disease, which is in fact the only disease to have been completely eradicated globally, should ever re-surface. Clearly the successful vaccination against covid-19 is a priority and... 

I shall discuss vaccines in the next installment...

Glossary of Terms (in order of appearance in the text)

Epidemic and pandemic (from the US center for disease control)

Occasionally, the amount of disease in a community rises above the expected level. Epidemic refers to an increase, often sudden, in the number of cases of a disease above what is normally expected (this called endemic)  in that population in that area. Outbreak carries the same definition of epidemic, but is often used for a more limited geographic area. Cluster refers to an aggregation of cases grouped in place and time that are suspected to be greater than the number expected, even though the expected number may not be known. Pandemic refers to an epidemic that has spread over several countries or continents, usually affecting a large number of people.

Filtering is simply a process by which small and large particles are separated. It is a slightly more sophisticated form of sieving in which a liquid is passed through a barrier (such as paper or a plastic mesh). The holes in the filter can be manufactured to allow (in this case) particles of less than 1000nm diameter through (the viruses), leaving the cells on the filter itself. 

RNA, DNA protein (these are discussed above), but formally, deoxyribonucleic acids differ chemically  from ribonucleic acids by virtue of a single oxygen atom per sugar (see RHS). One of the consequences of this difference is that DNA molecules form Watson and Crick based paired double helices, whereas RNA molecules form heterogeneous mixtures of helical regions and single-strands. In both bacterial and mammalian cells Francis Crick proposed the central dogma of molecular biology which states that DNA makes RNA (the process called transcription) makes protein (the process of translation). In the case of retroviruses, by definition, the genomic RNA must first be turned into DNA (through the action of the enzyme Reverse Transcriptase) before the proteins that make up the viral coat can be expressed in the host cell. 

Replication is the term used to describe the duplication of a genome. In the case of DNA genomes, the enzyme DNA polymerase (which varies considerably in its complexity, from bacteria to man, but is renowned for making very few mistakes) catalyses the copying of DNA to generate new chromosomes. In the case of viral replication, many copies of the viral genome must be replicated to be packaged into the viral capsid (protein shell) or envelope (protein and lipid coat). The original concept of replication was suggested by Watson and Crick in 1953 and through teh pioneering work of (Arthur) Kornberg and Meselson and Stahl, we now have a good understanding of the molecular basis of DNA replication as shown diagrammatically on the left. If the genome is made from RNA instead of DNA, replication is much more like transcription and since he transcribing enzyme, RNA polymerase is more careless than DNA polymerase, mutations arise more frequently in RNA viruses.

Thanks for the request from Anudhi regarding the specifics of replication in corona viruses, here is a summary of the properties of the Replicase gene. Like many RNA viruses, the proteins encoded in the RNA are expressed as a poly-protein which requires processing by a protease prior to assembly of the functional protein: in this case the replicase. The two replicase proteins combine to catalyse both transcription of the viral genome and replication in order that the genome can be packaged following assembly of new virus particles. The genome is just less than 30 000 nucleotides and an overview of the related SARS corona-virus can be found here for those of you who want more details.